Коэффициент Шарпа, (если хотите — Sharpe Ratio) был разработан в 1966 году лауреатом нобелевской премии Вильямом Шарпом и применяется для того, чтобы измерять уровни риска в инвестиционных портфелях.
Данный коэффициент является показателем инвестиционного актива (портфеля) и вычисляется в виде отношения усредненной премии за риск к усредненному отклонению актива (портфеля). В итоге, чем коэффициент выше, тем будут лучше результаты, показывающие по отношению к выбранным рискам инвестиционный актив.
Sharpe Ratio используют, чтобы определить насколько хорошо доходность от инвестиционного портфеля будет компенсировать принимаемый инвесторами риск. Другими словами, если сравнивать два актива с ожиданием одинаковых доходов, то вложение портфеля с более высоким показателем коэффициента Шарпа будет не таким рискованным.
Помимо этого, коэффициент Шарпа наглядно показывает, связан ли результат вложения инвестиций с чрезмерным риском или с досконально продуманным решением.
Коэффициент Шарпа, как же его определить? Формула расчета
Формула, по которой определяется (рассчитывается) Коэффициент Шарпа (Shаrpe Ratiо) достаточно проста.
Для начала необходимо определить безрисковую процентную ставку из рентабельности актива, к примеру, ту, что предлагается облигация министерства финансов США. После этого полученный результат поделить на стандартное отклонение портфельной прибыли (что такое стандартное отклонение смотрите ниже).
Формула расчета коэффициента, такова:
SR – коэффициент Shаrpe Ratiо;
Rp – ожидаемая прибыльность актива (т.е. портфеля);
Rf – % -ая ставка без риска;
? – сигма, стандартное отклонение.
Числитель является средним значением разницы за 36 месяцев доходности фонда с безрисковой ставкой, которая равна ставке рефинансирования.
В знаменателе стоит стандартное отклонение, являющееся мерой риска, другими словами вероятностью того, что полученная в будущем инвесторами доходность будет отличной от ожидаемой средней за 36 месяцев доходности.
Видео: Определяем эффективность стратегий торговли по коэффициенту Шарпа
http://www.youtube.com/watch?v=0Gft9AWrP_g
Что такое стандартное отклонение — ? и как оно влияет на работу коэффициента Шарпа?
В финансовом мире стандартное отклонение зачастую обозначают греческой буквой «?» (сигма, как в случае с коэффициентом Шарпа) и используют для того, чтобы оценить волатильность инвестиций.
Определить волатильность посредством стандартного отклонения – дело очень сложное, но нас это на данный момент не должно сильно беспокоить.
Важная особенность данного измерения (определения) – это, то насколько вырастает либо понижается доходность вашего актива в сравнении с его средней доходностью за некий определенный период времени.
Если говорить проще, то в случаях, когда доходность имеет такую волатильность, при которой она вырастает и понижается в значительной мере – Ваш инвестиционный портфель подвержен более высоким рискам, так как его исполнение может попасть под достаточно быстрое изменение в любую из сторон, как благоприятную, так и наоборот.
Объяснение формулы расчета по коэффициенту Шарпа
Формула расчета данного коэффициента на первый взгляд кажется, довольно замысловатой и многих заставляет паниковать. Не стоит этого делать – сама концепция очень проста.
Если смотреть с практической стороны, тогда Коэффициент Шарпа попросту определяет доходность имеющегося инвестиционного портфеля. Рассмотрим подробнее.
Первая (верхняя) строка формулы с «Rp–Rf», определяет величину процентной ставки и ежегодную доходность актива, получаемую вами после простой покупки ценных бумаг, скажем казначейства США, сроком на три месяца.
Таким образом, используя эту формулу, вы можете определить, имеет ли место в вашей стратегии прибыль либо стоит о ней забыть и приобрести векселя казначейства какой-либо другой страны, предположим вашей.
Допустим, что выбранная вами стратегия приносит достаточную прибыль, т.е. большую, чем процентная ставка векселей казначейства США. И тут коэффициент Шарпа задает вам следующий вопрос – вы получаете больше доходов благодаря своим умениям либо причиной тому больший риск? Для ответа на данный вопрос следует разделить первую (верхнюю) часть формулы т.е. «Rp–Rf» на сигму «?».
Таким образом, коэффициент показывает инвесторам две основные вещи. Во-первых, приносят либо нет их инвестиционные портфели большее количество денег, нежели безрисковая % ставка. И во-вторых, инвесторы видят прямое соотношение доходности вложений к прямым рискам.
Получается, что наш коэффициент показывает – торгуете ли вы с умом либо же просто рискуете, т.е. доходность вашего фонда, которая взвешена по риску.
Как использовать уже рассчитанный (определенный) коэффициент Шарпа?
Данный коэффициент рекомендовано применять на минимум трехлетней или четырехлетней истории работы инвестиционного актива.
Следует помнить, что стандартное отклонение рассчитывает абсолютную величину волатильности инвестиционного портфеля не связанную ни с одним из каких-либо индексов. Поэтому без дополнительной информации вы не сможете определить, является ли наш Коэффициент Шарпа со значением 1,06 для вас хорошим или плохим.
Относительно риска, оценку прибыльности своих инвестиций Вы сможете получить, лишь сравнив данный коэффициент у разных активов. Используя другие измерения совместно с Sharpe Ratio, инвесторы могут выбрать именно ту стратегию, которая будет подходить под их финансовые нужды и соответствовать граничным рискам.
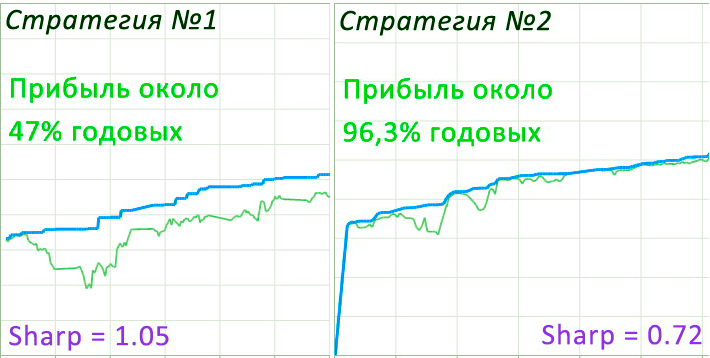
Применяя Коэффициент Шарпа, трейдеры имеют возможность между собой сравнить несколько стратегий.
К примеру, если сравнивать две системы, которые за определенный период показали одинаковую доходность, но при этом у одной из них риск получился больше (например, у первой), то соответственно у нее коэффициент по Шарпу будет меньше, то это говорит о ее низкой эффективности в сравнении со второй системой.
Данный коэффициент, как вариант, можно было бы применять для определения управляющих, которые предоставляют возможность копировать их сделки или для сравнения эффективности каких-либо стратегий с разными Памм счетами.
Но во втором случае трейдерам придется использовать лишь одну торговую стратегию, у которой имеется информация о валютном инструменте, на котором собственно и проводятся торги. А сделать это очень непросто, так как прибыльные Памм управляющие, как правило, торгуют активами и дополнительной информацией о них вряд ли поделятся.
Что же касается копирования сделок, то использование Sharpe Ratio здесь подходит лучшим образом, т.к. в большинстве случаев торговые сигналы поступают по определенной валютной паре, поэтому пользователям, которые их используют, расчеты (определяющие эффективность торговли управляющего) будет сделать намного проще.
Помимо этого, сегодня существуют сервисы, указывающие в статистике торговли управляющих уже готовый показатель Sharpe Ratio.
Помимо этого, формула расчета данного коэффициента предполагает применение бенчмарка, используемого в качестве предела, который должна превзойти конкретная стратегия (иначе нет смысла ее рассматривать).
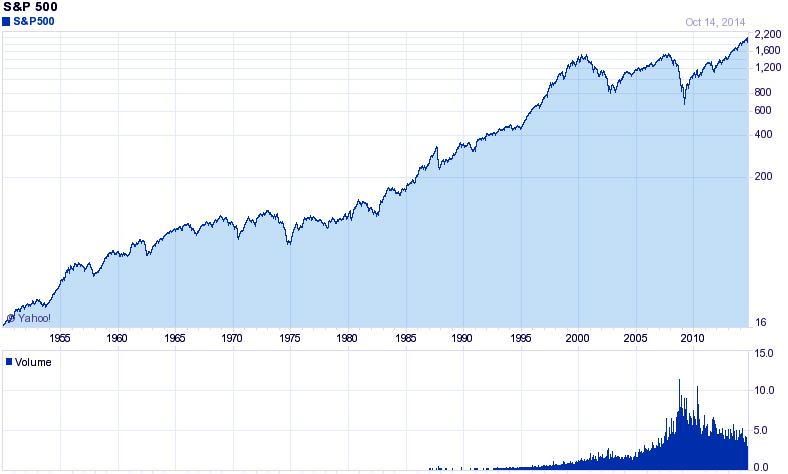
К примеру, простейшая стратегия «только лонг», выбранная для акций большой капитализации Штатов, должна надеяться, что в среднем преодолеет индекс «S&P 500» либо хотя бы с ним сравнится при меньшей волатильности по доходности.
При этом выбор бенчмарка не всегда дело очевидное. К примеру, может ли быть использован в роли бенчмарка для индивидуальных акций ETF сектора или лучше взять непосредственно «S&P 500»? А может лучше «Russel 3000»?
Также возникают сложности с «безрисковыми ставками» — можно ли использовать правительственные национальные долговые бумаги или корзину международных таких же долговых бумаг? Долгосрочные или краткосрочные ноты? А может смесь всего? Понятно, что способов выбрать бенчмарк огромное количество.
Коэффициент Шарпа, как правило, применяет безрисковые ставки, и зачастую для стратегий с использованием американских акций они основаны на правительственных казначейских 10-тилетних облигациях.
Недостатки и ограничения коэффициента Шарпа
При всех положительных показателях Sharpe Ratio небезупречен. Прежде всего, это связано с расчетом входных параметров.
К примеру, определение риска (стандартное отклонение в прибыльности актива) – вопрос спорный. А дело здесь в том, что у фондов с разными колебаниями доходности (положительные/отрицательные) при прочих равных могут быть близкими по значению показатели «?», а это совершенно не корректно с инвестиционной стороны.
Коэффициент Шарпа имеет еще один существенный недостаток – он поддается манипулированию. Другими словами значение коэффициента не будет показательным при крайне стабильных результатах.
Вернее, если фонд из месяца в месяц работает все время одинаково (схожие показатели доходности, которые превышают значения безрисковых ставок), то его значение коэффициента Шарпа будет запредельно высоко и ничего не скажет нам о действительном положении вещей. Это является следствием того, что стандартное отклонение неизменно будет стремиться к нулевому значению, а дробь – к бесконечности. Хотя сам факт стабильной прибыльности – уже большой плюс для инвесторов, главное в этом случае, чтобы доходы были выше банковских.
Безусловно, коэффициент Шарпа широко применяется в количественных финансах, однако у него имеются и свои ограничения.
Первым делом необходимо отметить, что Sharpe Ratio на данные прошлых событий. Его можно определить по волатильности и распределению исторических результатов, а не по тем событиям, которые ожидаются в будущем. Когда делают оценку инвестиционного портфеля по данному коэффициенту, предполагается, что будущие события будут подобны прошлым. А это, как вы знаете, не всегда так, в особенности, когда происходит изменение рыночных условий.
Также расчет коэффициента Шарпа предусматривает, то что используемые для этого результаты будут иметь нормальное по Гауссу распределение. Но, к огромному сожалению, нынешние рынки зачастую подвергаются более высокому эксцессу, чем при нормальном распределении. По этой причине у распределения результатов имеются так называемые «тяжелые хвосты», а уже экстремальные события происходят намного чаще, нежели предполагает распределение Гаусса.
Отсюда вывод – Sharpe Ratio недостаточно хорошо может оценить хвостовой риск.
Коэффициент Шарпа (eng. Sharpe Ratio), как определить его.
Формула коэффициента для расчета
РЕКОМЕНДУЕМ ПОСМОТРЕТЬ:


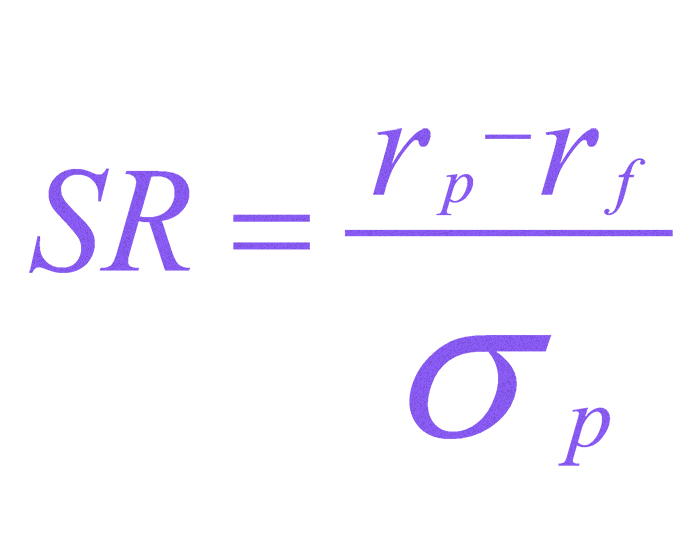

 Как точно определить тени свечей? Рассказываем за 3 минуты
Как точно определить тени свечей? Рассказываем за 3 минуты Проторговка на Forex: что это и как правильно действовать трейдеру?
Проторговка на Forex: что это и как правильно действовать трейдеру? Торговля на пробой и отбой (отскок) уровня. Лучшие стратегии и методы Форекс
Торговля на пробой и отбой (отскок) уровня. Лучшие стратегии и методы Форекс Как исполняются ордера на бирже Форекс? Варианты исполнения торговых приказов
Как исполняются ордера на бирже Форекс? Варианты исполнения торговых приказов Форекс паттерны
Форекс паттерны Стратегии Форекс, торговые методы прибыльного трейдинга
Стратегии Форекс, торговые методы прибыльного трейдинга